7/15 15:00 ~ 7/16 15:00에 진행된 SCPC 2022 1차 예선에 참여해보았습니다.

예년에 비해 난이도가 올라간 것 같다는 느낌을 받았습니다.
(제출횟수랑 남은 시간이 더 많이 남은건 아이러니하네요)
3번까지 꽤 빠르게 풀었는데, 4, 5번에서 고민을 조금 오래했습니다.
5번은 왜 맞았는지 모르겠어요
1. 개미
문제 요약
개미의 위치가 Pi, 개미가 들고 있는 값이 Vi일 때, 개미들을 Vi 오름차순으로 정렬하여 각 Pi자리에 하나씩 놓으려고 한다.
이때 개미의 이동 거리를 최소화 하라
풀이
Vi 순(같다면 Pi 순) 정렬을 한 후의 P 배열을 P'i라 할 때 $\sum_i {\left( P_i - P'_i \right) }$를 구하면 된다.
소스코드
#include <bits/stdc++.h>
typedef long long ll;
const ll M = 1e9 + 7;
using namespace std;
int main() {
ll T;
scanf("%lld", &T);
for (ll ca = 0; ca < T;) {
printf("Case #%lld\n", ++ca);
ll n;
scanf("%lld", &n);
vector<ll> v(n);
vector<pair<ll, ll>> p(n);
for (auto& t : v) scanf("%lld", &t);
for (ll i = 0; i < n; ++i) scanf("%lld", &p[i].first), p[i].second = v[i];
sort(p.begin(), p.end());
ll ans = 0;
for (ll i = 0; i < n; ++i) {
ans += abs(p[i].second - v[i]);
}
printf("%lld\n", ans);
}
}
2. K 등분
문제 요약
수열을 남김없이 연속된 K조각으로 나누고 이때 각 조각의 원소 합이 모두 같게 만드는 방법의 수를 구하여라
풀이
$C = TOTAL / K$라 가정하자. 나뉠 수 있는 구간은 0부터의 누적합이 C, 2C, ..., KC, (K+1)C, ...인 지점들이다.
dp를 사용하는데, dp[i]는 같은 값으로 나뉜 구간이 i개일 때의 경우의 수이다.
- dp[0] = 1
- iC인 지점에서 dp[i] += dp[i-1]
C는 양수, 음수일 때 위의 방법으로 구해지지만 0인 경우에 대해서도 고려해야 한다.
누적합이 0인 구간의 개수가 p일 때 확률과 통계에서 배운대로 구하자면 답은 아래와 같다
$`_{p-1}C_{k-1}$
소스코드
#include <bits/stdc++.h>
typedef long long ll;
const ll M = 1e9 + 7, N = 1e6 + 7;
ll inv[N] = { 0,1 }, fac[N] = { 1,1 }, ifac[N] = { 1,1 };
using namespace std;
int main() {
for (int i = 2; i < N; ++i) inv[i] = inv[M % i] * (M - M / i) % M, fac[i] = (i * fac[i - 1]) % M, ifac[i] = (inv[i] * ifac[i - 1]) % M;
ll T;
scanf("%lld", &T);
for (ll ca = 0; ca < T;) {
printf("Case #%lld\n", ++ca);
ll n, k;
scanf("%lld%lld", &n, &k);
vector<ll> v(n), c(n, 0);
for (int i = 0; i < n; ++i) scanf("%lld", &v[i]), c[i] = (i ? (c[i - 1] + v[i]) : v[i]);
if (c[n-1] % k) { puts("0"); continue; }
vector<ll> t(k + 1, 0); t[0] = 1;
ll C = c[n - 1] / k, p = 0;
if (C == 0) p -= k;
for (int i = 0; i < n; ++i) {
if (C > 0) {
if (c[i] > 0 && c[i] % C == 0) {
ll j = c[i] / C;
if (j > k) continue;
if (i == n - 1) p = t[k - 1] % M;
t[j] = (t[j] + t[j - 1]) % M;
}
}
else if (C < 0) {
if (c[i] < 0 && c[i] % C == 0) {
ll j = c[i] / C;
if (j > k) continue;
if (i == n - 1) p = t[k - 1] % M;
t[j] = (t[j] + t[j - 1]) % M;
}
}
else {
if (c[i] == 0) {
++p;
}
}
}
if (C) printf("%lld\n", p);
else if (p < 0) puts("0");
else printf("%lld\n", fac[p + k - 1] * ifac[k - 1] % M * ifac[p] % M);
}
}
3. 직교 다각형
문제 요약
격자판에서 정점들이 주어질 때, 문제에 해당하는 직교다각형을 그리고 그 테두리의 총 길이를 구하여라.
단, 최대 1개의 오류 정점이 있을 수 있다.
풀이
직교다각형의 오류 정점을 찾는것은 매우 쉽다. 무조건 각 row, col에서의 점 개수가 짝수여야되는데, (홀수 row, 홀수 col)점을 구해서 지우면 된다.
남은 점들에 대해서 다음 그림을 보면 이해가 쉬울 것 같다.
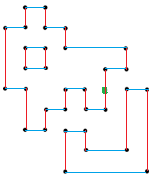
인접한 가로/세로 두 점씩 이으면 된다.
소스코드
#include <bits/stdc++.h>
typedef long long ll;
const ll M = 1e9 + 7;
using namespace std;
int main() {
ll T;
scanf("%lld", &T);
for (ll ca = 0; ca < T;) {
printf("Case #%lld\n", ++ca);
ll n;
scanf("%lld", &n);
vector<pair<ll, ll>> v(n);
map<ll, ll> mpx, mpy;
for (auto& [a, b] : v) scanf("%lld%lld", &a, &b), mpx[a]++, mpy[b]++;
ll Ex = 0, Ey = 0;
for (auto& [x, y] : mpx) if (y & 1) Ex = x;
for (auto& [x, y] : mpy) if (y & 1) Ey = x;
sort(v.begin(), v.end(), [](pair<ll, ll> x, pair<ll, ll> y) {return x.first < y.first || (x.first == y.first && x.second < y.second); });
ll s = 0, t = 0, p = 0, c;
for (auto& [x, y] : v) {
if (x == Ex && y == Ey) continue;
if (s != x) {
s = x;
t = 1;
c = y;
}
else {
if (t == 1) p += y - c;
else c = y;
t = !t;
}
//printf("%lld %lld %lld %lld %lld\n", x, y, t, p, c);
}
sort(v.begin(), v.end(), [](pair<ll, ll> x, pair<ll, ll> y) {return x.second < y.second || (x.second == y.second && x.first < y.first); });
s = 0;
for (auto& [x, y] : v) {
if (x == Ex && y == Ey) continue;
if (s != y) {
s = y;
t = 1;
c = x;
}
else {
if (t == 1) p += x - c;
else c = x;
t = !t;
}
}
printf("%lld\n", p);
}
}
4. 지우개
문제 요약
a, b로 이루어진 두 문자열 X, Y가 주어진다.
X에 대해서 가장 앞 혹은 뒤의 a 혹은 b를 지울 수 있을 때, Y를 만들 수 있는지 여부를 확인하라
풀이
KMP인걸 알 수 있다. 우선 X와 Y를 연속한 a, b의 개수들로 압축한다. (ex) aaaa -> (a,4))
Y에 대해서 가장 앞의 두 값과 가장 뒤의 두 값을 일단 따로 저장하고 떼어낸다. (ex) (a,1),(b,1),(a,2),(b,1),(a,1) -> (a,2))
Y의 개수가 부족하면 2개 이하로 뗄 수도 있다. 이를 Y'이라 하자.
KMP를 이용하여 X에서 Y'의 인덱스 i들을 찾는다. 위에서 따로 저장해둔 앞/뒤 2개의 값을 다음과 같이 처리한다.
앞만 예시로 들어보자면,
저장한 값이 1개일 때, [0,i-1]에서 저장한 값과 같은 알파벳이 저장한 값보다 많이 나오면 ok
저장한 값이 2개일 때, [0,i-2]에서 먼저 저장한 값(a,1)과 같은 알파벳이 저장한 값보다 많이 나오고 i-1의 알파벳이 나중에 저장한 값(b,1)과 같으며 그 개수보다 많으면 ok
이를 뒤에서도 마찬가지로 해보고 양쪽이 ok면 YES
소스코드
#include <bits/stdc++.h>
typedef long long ll;
const ll M = 1e9 + 7, N = 1e6 + 7;
using namespace std;
char s1[N], s2[N];
pair<int, int> v1[N], v2[N], st[2], ed[2];
int f[N] = { -1 }, e[N][2];
int main() {
ll T;
scanf("%lld", &T);
for (ll ca = 0; ca < T;) {
printf("Case #%lld\n", ++ca);
int n = 0, m = 0;
scanf("%*d%*d\n%s\n%s", s1, s2);
char s; int c;
s = s1[0], c = 1;
for (int i = 1; s1[i]; ++i) {
if (s == s1[i]) ++c;
else v1[n++] = { s == 'b',c }, s = s1[i], c = 1;
}
v1[n++] = { s == 'b',c };
int cs = 0, ce = 0;
s = s2[0], c = 1;
for (int i = 1; s2[i]; ++i) {
if (s == s2[i]) ++c;
else {
if (cs < 2) st[cs++] = { s == 'b',c };
else v2[m++] = { s == 'b',c };
s = s2[i], c = 1;
}
}
if (m) ed[ce++] = v2[--m], v2[m] = { 0,0 };
ed[ce++] = { s == 'b',c };
for (int i = 1; i <= n; ++i) {
e[i][0] = e[i - 1][0];
e[i][1] = e[i - 1][1];
e[i][v1[i - 1].first] += v1[i - 1].second;
}
int pr = 0;
if (m) {
for (int i = 0, j = -1; i < m; f[++i] = ++j) while (~j && v2[i] != v2[j]) j = f[j];
for (int i = 0, j = 0; i < n; ++i) {
//printf("%d %d\n", i, j);
while (~j && v1[i] != v2[j]) j = f[j];
//printf("%d %d\n", i, j);
if (++j == m) {
int X = i + 1 - j, Y = i + 1;
int ch = 0;
if (cs == 0) ch++;
else if (cs == 1) ch += (e[X][st[0].first] >= st[0].second);
else if (cs == 2 && X) ch += (e[X - 1][st[0].first] >= st[0].second && v1[X - 1].first >= st[1].first && v1[X - 1].second >= st[1].second);
if (ce == 1) ch += (e[n][ed[0].first] - e[Y][ed[0].first] >= ed[0].second);
else if (ce == 2 && Y < n) ch += (v1[Y].first == ed[0].first && v1[Y].second >= ed[0].second && e[n][ed[1].first] - e[Y + 1][ed[1].first] >= ed[1].second);
if (ch == 2) { pr = 1; break; }
}
}
}
else {
for (int i = 0; i < n; ++i) {
int X = i, Y = i;
int ch = 0;
if (cs == 0) ch++;
else if (cs == 1) ch += (e[X][st[0].first] >= st[0].second);
else if (cs == 2 && X) ch += (e[X - 1][st[0].first] >= st[0].second && v1[X - 1].first >= st[1].first && v1[X - 1].second >= st[1].second);
if (ce == 1) ch += (e[n][ed[0].first] - e[Y][ed[0].first] >= ed[0].second);
else if (ce == 2 && Y < n) ch += (v1[Y].first == ed[0].first && v1[Y].second >= ed[0].second && e[n][ed[1].first] - e[Y + 1][ed[1].first] >= ed[1].second);
if (ch == 2) { pr = 1; break; }
}
}
puts(pr ? "YES" : "NO");
}
}
5. 독립
문제 요약
격자점 가장 왼쪽 위(0,0)에서 가장 오른쪽 아래(n-1,n-1)로 우측 하단 방향으로만 이동 가능하다.
(0,0)에서 (n-1,n-1)사이의 최단경로들이 존재하는데, 같은 경로에 존재할 수 없는 두 점의 쌍들의 개수를 구하여라.
풀이
우리가 중학교 때 배우는 확률과 통계쪽의 격자점 최단 경로 찾기와 비슷하다.
$DP_{i,j} = DP_{i-1,j} + DP_{i,j-1} + 1 - DP_lca$ 이때 lca는 (i-1,j)와 (i,j-1)이 공통으로 경유하는 가장 가까운 지점이다.
lca를 구하는 방법은 (i-1,j)는 최대한 j를 줄이고 (i,j-1)은 최대한 i를 줄였을 때 처음으로 만나는 지점을 구할 수 있다.
소스코드
#include <bits/stdc++.h>
typedef long long ll;
const ll M = 1e9 + 7, N = 2010;
using namespace std;
char s[N];
ll arr[N][N], e[N][N];
int main() {
ll T;
scanf("%lld", &T);
for (ll ca = 0; ca < T;) {
printf("Case #%lld\n", ++ca);
ll n, m = 0;
scanf("%d", &n);
for (ll i = 0; i < n; ++i) {
scanf("\n%s", s);
for (ll j = 0; j < n; ++j) m += (arr[i][j] = (s[j] == '.'));
}
pair<ll, ll> u, l;
for (ll i = 0; i < n; ++i) {
for (ll j = 0; j < n; ++j) {
if (!arr[i][j]) continue;
u = l = { -1,-1 };
if (i && arr[i - 1][j]) u = { i - 1,j };
if (j && arr[i][j - 1]) l = { i,j - 1 };
if (u.first == -1 && l.first == -1) e[i][j] = 1;
else if (u.first == -1) e[i][j] = e[l.first][l.second] + 1;
else if (l.first == -1) e[i][j] = e[u.first][u.second] + 1;
else {
e[i][j] = e[u.first][u.second] + e[l.first][l.second] + 1;
while (u != l) {
if (u.second && arr[u.first][u.second - 1]) --u.second;
else --u.first;
if (l.first && arr[l.first - 1][l.second]) --l.first;
else --l.second;
}
e[i][j] -= e[u.first][u.second];
}
}
}
ll p = m * (m - 1) / 2 + m;
for (ll i = 0; i < n; ++i) for (ll j = 0; j < n; ++j) if(arr[i][j]) p -= e[i][j];
printf("%lld\n", p);
}
}'PS > Competition' 카테고리의 다른 글
| ICPC 2022 예선 후기 (8) | 2022.10.08 |
|---|---|
| Meta Hacker Cup 2022 후기 (0) | 2022.09.12 |
| UCPC 2022 예선 후기 (2) | 2022.07.11 |
| 진짜 최종 구데기컵 2 2 검수 후기 (2) | 2022.04.10 |
| ICPC 2021 후기 (0) | 2021.11.15 |



