Recurrence Relations and Recursive Algorithms
Recurrence Relations
recurrence relations (difference equation)
- for a n.f. $(a_0,a_1,\cdots ,a_r,\cdots )$, an equation relating $a_r$ for any $r$ to one or more of $a_i$ ($i<r$)
- also called difference equation
boundary condition : values of function at one or more points so that initialtize the function
linear recurrence relation with constant coefficients (LRRwCC) : $C_0a_r + C_1a_{r-1}+\cdots +C_ka_{r-k} = f(r)$
kth-order recurrence relation
- ex) $2a_r+3a_{r-1} =2r$ : first order LRRwCC
- the values of k consecutive $a_i'$s
- Fewer than k values of n.f. will not be sufficient to determine function uniquely
- More than k values of n.f. might make it impossible for existence of n.f.
solution of linear difference equation with constant coefficients
- homogeneous solutoin $a^{(h)} = (a_0^{(h)}, a_1^{(h)}, \cdots , a_r^{(h)}, \cdots )$
$C_0 a_r^{(h)} + C_1 a_{r-1}^{(h)} + \cdots + C_k a_{r-k}^{(h)} = 0$
- particular solution $a^{(p)} = (a_0^{(p)}, a_1^{(p)}, \cdots , a_r^{(p)}, \cdots )$
$C_0 a_r^{(p)} + C_1 a_{r-1}^{(p)} + \cdots + C_k a_{r-k}^{(p)} = f(r)$
- total solution $a=a^{(h)}+a^{(p)}$
$C_0 (a_r^{(h)} +a_r^{(p)}) + C_1 (a_{r-1}^{(h)} + a_{r-1}^{(p)}) + \cdots + C_k (a_{r-k}^{(h)} + a_{r-k}^{(p)}) = f(r)$
Homogeneous Solutions
Substituting $A\alpha^r$ for $a_r$
$C_0 A\alpha^r+C_1A\alpha^{r-1}+\cdots +C_kA\alpha^{r-k}=0$
simplified to
$C_0 \alpha^r+C_1\alpha^{r-1}+\cdots +C_k\alpha^{r-k}=0$
$\alpha_1$ is one roots of characteristic equation (characteristic root)
$a_r^{(h)} = A_1\alpha_1^r+A_2\alpha_2^{r-1}+\cdots +A_k\alpha_k^{r-k}$
if $\alpha_1$ is root of multiplict m,
$a_r^{(h)} = (A_1r^{m-1}+A_2r^{m-2}+\cdots +A_{m-1}r+A_m)\alpha_1^r$
Particular Solutions
There is no general procedure for determining particular solution of difference equation
when $f(r)$ is of the form of polynomial of degree $t$ in $r$
$F_1r^t +F_2r^{t-1}+\cdots + F_tr+F_{t+1}$
corresponding particular solution will be of the form
$P_1r^t +P_2r^{t-1}+\cdots + P_tr+P_{t+1}$
when $f(r)$ is of the form of $\beta^r$
corresponding particular solution will be of the form $P\beta^r$ if $\beta$ is not a characteristic root
when $f(r)$ is of the form of
$(F_1r^t +F_2r^{t-1}+\cdots + F_tr+F_{t+1})\beta^r$
i) If $\beta$ is not a characteristic root, corresponding particular solution is of the form
$(P_1r^t +P_2r^{t-1}+\cdots + P_tr+P_{t+1})\beta^r$
ii) If $\beta$ is characteristic root or multiplicity m, corresponding particular solution is of the form
$r^m(P_1r^t +P_2r^{t-1}+\cdots + P_tr+P_{t+1})\beta^r$
Total Solutions
just put both homogeneous and particular solution in together
$a_r = a_r^{(h)} + a_r^{(p)}$
Solution by Method of Generation Functions
general procudre for determining generating functino of numerif function a from difference equation
$C_0a_r + C_1a_{r-1}+\cdots +C_ka_{r-k} = f(r)$
multiplying both sides of equation by $z^r$ and summing from $r=s$ to $r=\infty$, we obtain
$\Sigma_{r=s}^\infty (C_0a_r + C_1a_{r-1}+\cdots +C_ka_{r-k})z^r = \Sigma_{r=s}^\infty f(r)z^r$

Matrix Multiplication Algorithms

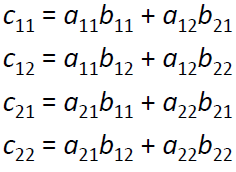 |
 |
| 4 addition 8 multiplication |
18 addition 7 multiplication |
i) classical multiplication
$n^3$ multiplication operations
$n^2(n-1)$ addition operations
$f_r=n^3+n^2(n-1)=O(n^3)$
ii) second method
Let $f_r$ denote total number of arithmetic operations required to multiply two $2^r\times 2^r$ matrics.
$f_r=6f_{r-1}+18\cdot 2^{2(r-1)}$, $r\geq 1$, $f_0=1$
$f_r = 7\cdot 7^r-(18/3)\cdot 4^r$
for $n=2^r$
$f_r =7\cdot 7^{\lg n} -(18/3)n^2 = O(n^{2.81})$
학교 강의를 토대로 개인 공부 목적으로 작성되어 오타가 및 오류가 있을 수 있으며, 문제가 될 시 삭제될 수 있습니다.
'Study > 이산수학' 카테고리의 다른 글
| Logic (0) | 2021.12.17 |
|---|---|
| Discrete Numeric Functions and Generating Functions (0) | 2021.12.13 |
| Analysis of Algorithms (2) | 2021.12.13 |
| Graphs (2) | 2021.12.13 |
| Relations and Functions (0) | 2021.12.12 |


