Boolean Algebra
Propositions and Well Formed Formulas
propositoin : declarative sentence that "must be true or false but not both"
logical connectives :
- ¬(not)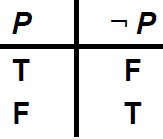 |
|
- $\vee$(or)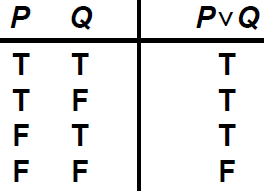 |
- $\Rightarrow$(implies)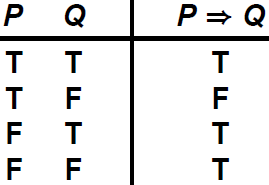 |
- $\wedge$(and)  |
- $\Leftrightarrow$(if and only if) |
Well Formed Formula (wff) : all propositional constants and T/F are wffs
tautology : 항등
contradiction : 모순
satisfiable wff : wff that is not a contradiction
Normal Forms and Boolean Algebra
design switching circuits using truth table
- switching function : mapping input to output given by truth table
- procedure
1) Obtain wff corresponds
2) Minimize this wff
3) Obtain the circuit
- notation switching
- $\wedge$ -> $\cdot$
- $\vee$ -> +
- propositional constant -> boolean value
- wff -> boolean expression
- connective -> operator
literal : either boolean variable or its complement
minterm : boolean expression which is conjuction of literals
maxterm : boolean expression which is disjunction of literals
clause : either dijunction or conjunction of literals
conjunctive normal form(CNF) : conjunction of clauses
disjunctive normal form(DNF) : disjunction of cluases
Procedure to obtain corresponding boolean expression
- using minterm
1) create minterm for each truth table row
2) take disjunction of minterms
- using maxterm
1) create maxterm for each truth table row
2) take conjunction of maxterms
or use karnaugh map
Boolean Algebra $(K,\cdot , +)$ following laws(Huntington's Postulates)
1. (Closure) $a\cdot b$, $a+b$ are in $K$
2. (Commutativity) $a\cdot b=b \cdot a$ and $a+ b=b+a$
3. (Distributivity) $a\cdot (b+c) = a\cdot b +a\cdot c$ and $a+ (b\cdot c) = (a+b)\cdot (a+c)$
4. (Identity and zero elements) $a\cdot 1=a$ and $a+0=a$
5. (Complement) for complement of $a$, $a\cdot \bar{a}=0$ and $a+\bar{a}=1$
6. There are at least two distinct elements a and b, $a\neq b$ in K
dual :
1. replace all $\cdot$ by $+$ and $+$ by $\cdot$
2. replace all 0 by 1 and 1 by 0
Boolean Algebra Theorem
1. identity and zero (1 and 0) are unique
2. $a\cdot a = a$ and $a+a=a$
3. $a\cdot 0 =0$ and $a+1=1$
4. $a$ have unique complement $\bar{a}$
5. $a=¬¬a$
6. $\bar{1}=0$ and $\bar{0}=1$
7. $\overline{a\cdot b} = \bar{a}+\bar{b}$ and $\overline{a+b} = \bar{a}\cdot\bar{b}$ (De Morgan's Law)
8. $a\cdot (b\cdot c) =(a\cdot b)\cdot c$ and $a+(b+c)=(a+b)+c$ (Associativity)
9. $a\cdot (a+b) = a$ and $a+(a\cdot b) =a$ (Absorption)
10. $a\cdot(\bar{a}+b)=a\cdot b$ and $a+(\bar{a}\cdot b)=a+b$
Proof Methods
Truth table method
- determine whether wff is tautology by using truth table for "premises=>conclusion"
- needs lots of rows(2^{# of constant} rows)
logical equivalance : two wffs $\alpha$ and $\beta$ are equivalent iff $\alpha\Leftrightarrow \beta$ is tautology
inference rule
- format : $\{\alpha_1,\alpha_2,\cdots ,\alpha_k\} |=\beta$ where $\alpha_i$s and $\beta$ are wffs
- interpretation : infer that $\beta$ is true once we have shown each of $\alpha_i$s is true
ex)
$\{\alpha,\beta\} |= \alpha \wedge\beta$
$\{\alpha,\beta\} |= \alpha$
$\{\alpha,\beta\} |= \beta$
$\{\alpha\}|=\alpha\vee\beta$
$\{\beta\}|=\alpha\vee\beta$
$\{\alpha,\alpha\Rightarrow\beta\}|=\beta$ modus ponens(MP)
$\{\bar{\beta},\alpha\Rightarrow\beta\}|=\bar{\alpha}$ modus tollens(MT)
$\{\bar{\alpha},\alpha\vee\beta\}|=\beta$ disjunctive syllogism(disj. syll.)
$\{\alpha\Rightarrow\beta ,\beta\Rightarrow\gamma\}|=\alpha\Rightarrow\gamma$ hypothetical syllogism(hypo. syll.)
$\{\alpha\Rightarrow\beta ,\gamma\Rightarrow\delta\}|=\alpha\wedge\gamma\Rightarrow\beta\wedge\delta$
$\{\alpha\vee\beta,\bar{\alpha}\vee\beta\}|=\beta$
- we see that $\alpha_1\wedge\alpha_2\wedge\cdots\wedge\alpha_k\Rightarrow\beta$
Truth method that may be used to show taht a wff is a tautology
Trivial Proof(tirv. pf.) : to show $\alpha_1\Rightarrow\alpha_2$, show $\alpha_2$ is tautology
- $\{\alpha_2\}|=\alpha_1\Rightarrow\alpha_2$
Vacuous Proof(vac. pf.) : to show $\alpha_1\Rightarrow\alpha_2$, show $\alpha_1$ is contradiction
- $\{¬\alpha_1\}|=\alpha_1\Rightarrow\alpha_2$
Direct Proof(dir. pf.) : to show $\alpha_1\Rightarrow\alpha_2$, assume $\alpha_1$ is true and this implies $\alpha_2$ is true
Indirect Proof(ind. pf.) : to show $\alpha_1\Rightarrow\alpha_2$, assume $\alpha_2$ is false and implies $\alpha_1$ also false
Proof by cases(by cases) : for $\alpha_1\vee\alpha_2\vee\cdots\vee\alpha_k\Rightarrow\beta$, show $\alpha_1\Rightarrow\beta, \cdots, \alpha_k\Rightarrow\beta$
Proof by contradiction(contr.) : to show $\alpha$ is true, first assume $\alpha$ is false and arrive contradiction
Tableau Method
tableau method
- mechanical procedure to determine if wff is tautology, contraadiction or satisfiable
- applied directly only to DNF wffs
c.f.) Davis-Putnam procudure requires CNF
- process into DNF
1. eliminate all occurance of $\Rightarrow$ and $\Leftrightarrow$ using $\alpha \Rightarrow \beta\equiv\bar{\alpha}\vee\beta$ and $\alpha\Leftrightarrow\beta\equiv(\alpha\Rightarrow\beta)\wedge(\beta\Rightarrow\alpha)$
2. repeatedly use De Morgan's laus so that resulting wff contains only literals and operator $\wedge$ and $\vee$
3. transform into DNF using $\alpha\wedge(\beta\vee\gamma)\equiv(\alpha\wedge\beta)\vee(\alpha\wedge\gamma))$
4. simplify wff resulting from 1~3 using $p\wedge p\equiv p$ and $\bar{p}\wedge\bar{p}\equiv\bar{p}$
- process into CNF
1. same as above
2. same as above
3. transform into CNF using $\alpha\vee(\beta\wedge\gamma)\equiv(\alpha\vee\beta)\wedge(\alpha\vee\gamma)$
4. simplify wff resulting from 1~3 using $p\vee p\equiv p$ and $\bar{p}\vee\bar{p}\equiv\bar{p}$
First Order Logic(FOL) / First Order Predicate Calculus
propositional logic isn't powerful enough to make all inferences that may be possible from given set of premises.
first order logic (FOL) ( = first order predicate calculus )
- wffs of first order logic contain predicates and quantifiers
predicates
- $P(x_1,x_2,\cdots,x_n),n>0$, mapping from $x_1,\cdots,x_n$ to values T/F
n: degree of predicate
P : symbol
x_i : parameters
quantifiers
- Universal $\forall$ : $\forall xP(x)$ : for all x, P(x) is true
- Existential $\exists$ : $\exists xP(x)$ : there exist x that make P(x) true
a wff of FOL
- all propositional constants, predicates, T/F are FOL wffs
- if a and b are FOL wffs, all basic representation of a and b are FOL wffs
- $\forall x (\alpha)$ and $\exists x (\alpha)$ are FOL wffs whenever $\alpha$ is FOL wff and x in not bound in $\alpha$
- nothing else is FOL wff

proof methods of FOL wffs
By Example : To show that $\exists x\alpha(x)$, sufficient to show $\alpha(x)$ is true for some x
By counter example : To show $\forall x \alpha(x)$ is false, sufficient to show $\alpha(x)$ is false for some x
By generalization : To show $\forall x \alpha(x)$ is true, sufficient to show $\alpha(x)$ is true for arbitrary x (!= some particular x)
학교 강의를 토대로 개인 공부 목적으로 작성되어 오타가 및 오류가 있을 수 있으며, 문제가 될 시 삭제될 수 있습니다.
'Study > 이산수학' 카테고리의 다른 글
| Recurrence Relations and Recursive Algorithms (0) | 2021.12.13 |
|---|---|
| Discrete Numeric Functions and Generating Functions (0) | 2021.12.13 |
| Analysis of Algorithms (2) | 2021.12.13 |
| Graphs (2) | 2021.12.13 |
| Relations and Functions (0) | 2021.12.12 |


