2021.08.14 11:00~16:00 5시간동안 진행되었다.

결과는 4솔브 중 1등 전체 40등
ABCD / EFGH / IJKL로 팀원을 나눴고 EFGH를 맡았다.
H번 문제를 보고 풀이가 바로 떠오르지 않아 다른 팀원에게 부탁했고 E, F를 보았다.
문제
E번을 보고 최근에 풀었던 Rock Paper Scissors / Swapping Places 두문제가 생각났었는데 사실 아무 관계 없는거같다.
대신 Swapping Places풀이에서 힌트를 살짝 얻은 것 같은데,
가위바위보에서 왼쪽에서 오른쪽으로 보면서 생각하면 RSSSSS같은경우 한번에 R이 맨 뒤로 가는걸 알 수 있는데, 이를 반대로 생각하면 S는 한번에 한칸 왼쪽으로 간다는 걸 알 수 있다.
T번 진행된다는 건 min(왼쪽으로 갈 수 있는 최대 칸수, T)에 해당하는 만큼 이동하게 된다는 뜻이고, T가 커봐야 N보다 작다는 걸 알 수도 있다.
시간복잡도 O(N)에 구할 수 있다.
F번 간단한 문제는 간단하지 않았다!
두 점 i와 j 간 거리가 min(|xi-xj|,|yi-yj|)라고 생각하면 된다.
이 경우 모든 i, j (1<=i,j<=n)에 대해서 거리들의 총합을 구하는 문제다.
임의의 점에 대해 생각해보자.
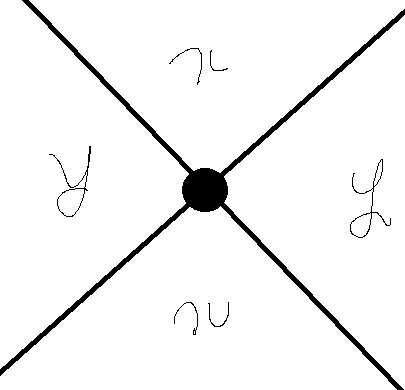
위 그림처럼 각 영역에서
상/하에 다른 점이 있는 경우 x축간 거리를 비교하면 되고,
좌/우에 다른 점이 있는 경우 y축간 거리를 비교하면 된다.
다른 점이 무조건 해당 점을 기울기 1로 지나는 직선 아래에 있다고 가정하자(우측/하단)
그런 경우 해당 점을 기울기 -1로 지나는 직선의 x절편을 기준으로 더 작다면 x축간 비교, 더 크다면 y축간 비교를 하면 된다.
이는 구간합을 이용해서 구할 수 있고, 대회에선 펜윅트리로 구현을 했었다.
해당 점에서의 계산을 할 때 우측/하단의 점들에 대해 사전 계산되어있어야 하는데 이는 점들을 기울기 1로 지나는 직선에 대해 y절편 기준 작은 값부터 정렬해두면 된다.
시간복잡도 O(NlgN)에 구할 수 있다.
후기
재미있는 문제가 많았다.
E, F번을 푸는데 시간을 너무 많이 쓴 것 같다.
F번 코드를 세 번 제출했는데 왜 틀렸는지 이유를 모르고 그냥 무작정 사이즈 한번 늘려보고 long long으로 바꾸니 맞았었다.
시간이 남았을 때 A번을 보고 풀이가 바로 생각나긴 했는데, 구현에 시간이 너무 걸릴 것 같아서 포기ㅡㅡ
G번을 보고 예선의 D번 풀이에서 조합론을 섞어서 조금만 바꾸면 되겠다 싶었는데 해설 들으니 전혀 아니었던 것 같다.
4솔브들 중 1등을 했었는데, 연습할때마다 페널티로 같은 솔브 수에서 등수가 밀렸던걸 이번엔 잘 풀어나갔던 것 같다.
아쉬웠던점은 A, J에서 반례를 못찾고 말려서 결국 해결 못했던 것.
대회를 대비해서 풀이를 생각해내는 시간이나, 구현 정확성?을 늘릴 수 있도록 연습하면 좋을 것 같다.
작년보다는 좋은 성과를 낼 수 있어 좋았고, 여전히 부족한 점이 많이 느껴져 아쉬웠다.